In general, bounding box techniques such as AABB are used to provide collision detection in 3D environments. Although the implementation and calculation time of these algorithms are fast, their sensitivity is not sufficient in applications where each triangle is important. If you want to cover details about you should visit this article. This article will show a simple implementation on OpenGL based on the intersection between triangle and point.
Triangle Point Intersection
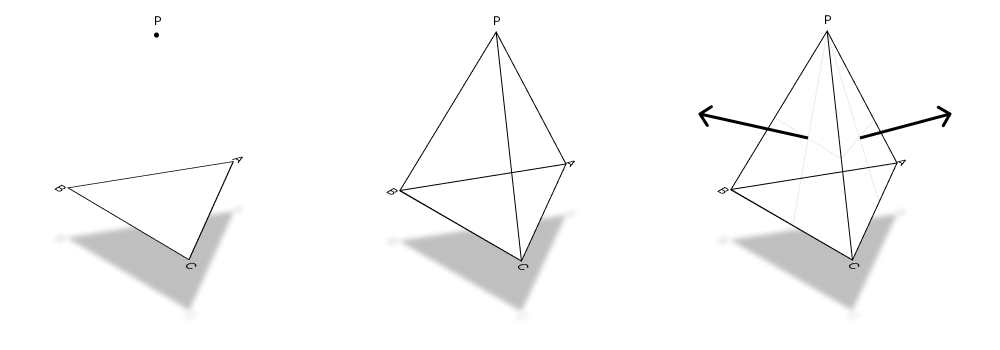
Triangles are basic shapes of 3D meshes and they are represented by three coplanar planes. For checking intersection we need to know position of 3 edges of triangles. We need some geometrical approach for checking intersection between triangle and point. If we create pyramid from point and triangle, we can check is pyramid faces are flat. Whether the surfaces between the pyramid and the point are parallel to each other tells us whether the point is inside the triangle. If all three surfaces of the pyramid are parallel to each other, the point is inside the triangle, otherwise the point is outside the triangle.
Lets say we have triagle named ABC and point P. When we create pyramid we will have PAB, PBC and PCA faces. For checking this faces direction, we need cross and dot products. Cross product gives us the normal of a triangle, and dot product gives us normals pointing direction. If those directions pointing same direction, point P is inside ABC triangle.
OpenGL Example
In order to better understand the intersection of triangle and point, the algorithm is shown with a cube and a point on OpenGL. You can download the codes as Visual Studio Solution from the repo in the link.

In order to separate the algorithm from OpenGL codes, the renderer pipeline is abstracted and called over different classes. Window creation with GLFW is done with the GLWindow class. Camera class, on the other hand, adjusts the camera’s point of view and position towards the object. In the Renderer class, objects are drawn into the created window by passing them through the renderer pipeline in line with the vertices and indices given. With the Shader class, the shader is created and compiled.
// Application.cpp
GLWindow gl_window;
Camera camera(
glm::vec3(100.0f, 0.0f, 200.0f),
glm::vec3(0.0f, 0.0f, 0.0f),
upVector, &gl_window.WIDTH, &gl_window.HEIGHT
);
Renderer cube(verticesCube, indicesCube);
Renderer point(pointVertices, pointIndices);
Shader shaderBasic("Basic.shader");
OpenGL draws triangles from vertex points and index points. Starting from here we can create triangles from vertex points. For this, a geometry header file has been created in which triangles and different geometric objects will be created.
// Geometry3D.h
#pragma once
#include <glm/glm.hpp>
#include "VertexBuffer.h"
typedef glm::vec3 Point;
struct Triangle
{
Point a;
Point b;
Point c;
Vertex& aV;
Vertex& bV;
Vertex& cV;
};
When creating objects from the renderer class, triangles are also created from indices and pushed into the m_vertices vector. With that way we can reach triangles and its vertex informations easily.
// Renderer.cpp
Renderer::Renderer(std::vector<Vertex>& vertices, std::vector<GLuint>& indices)
: m_vertices(vertices)
, m_indices(indices)
{
std::cout << "Renderer Constructor" << std::endl;
va.Bind();
for (int i = 0; i < m_indices.size(); i++)
{
Point a = m_vertices[m_indices[i]].position;
Vertex& aV = m_vertices[m_indices[i]];
i++;
Point b = m_vertices[m_indices[i]].position;
Vertex& bV = m_vertices[m_indices[i]];
i++;
Point c = m_vertices[m_indices[i]].position;
Vertex& cV = m_vertices[m_indices[i]];
Triangle tri = { a, b, c, aV, bV, cV };
m_triangles.push_back(tri);
}
vb = new VertexBuffer(m_vertices);
ib = new IndexBuffer(m_indices);
va.AddBuffer(*vb, 0, 3, sizeof(Vertex), (void*)0);
va.AddBuffer(*vb, 1, 3, sizeof(Vertex), (void*)(3 * sizeof(float)));
va.AddBuffer(*vb, 2, 3, sizeof(Vertex), (void*)(6 * sizeof(float)));
va.Unbind();
vb->Unbind();
ib->Unbind();
}
All triangles and its necessary items are created. Now we can create one point and we can check intersection of that point with triangle in main loop.
Point p;
while (!glfwWindowShouldClose(gl_window.window))
{
gl_window.Bind();
shaderBasic.SetUniform3f("lightPos", 0.0f, 0.0f, 0.0f);
shaderBasic.SetUniform3f("lightColor", 0.8f, 0.8f, 0.8f);
cube.Clear();
point.Clear();
camera.UpdateProjMatrix();
proj = camera.GetProjMatrix();
view = camera.GetViewMatrix();
if (glfwGetKey(gl_window.window, GLFW_KEY_W) == GLFW_PRESS) {
pointPos.x += 0.1f;
}
else if (glfwGetKey(gl_window.window, GLFW_KEY_S) == GLFW_PRESS) {
pointPos.x -= 0.1f;
}
else if (glfwGetKey(gl_window.window, GLFW_KEY_A) == GLFW_PRESS) {
pointPos.y += 0.1f;
}
else if (glfwGetKey(gl_window.window, GLFW_KEY_D) == GLFW_PRESS) {
pointPos.y -= 0.1f;
}
else if (glfwGetKey(gl_window.window, GLFW_KEY_E) == GLFW_PRESS) {
pointPos.z += 0.1f;
}
else if (glfwGetKey(gl_window.window, GLFW_KEY_Q) == GLFW_PRESS) {
pointPos.z -= 0.1f;
}
p = pointPos;
for (int i = 0; i < cube.m_triangles.size(); i++)
{
bool isCollided = CheckPointInTriangle(p, cube.m_triangles[i]);
if (isCollided)
{
cube.m_triangles[i].aV.color = glm::vec3(1.0f, 1.0f, 1.0f);
cube.m_triangles[i].bV.color = glm::vec3(1.0f, 1.0f, 1.0f);
cube.m_triangles[i].cV.color = glm::vec3(1.0f, 1.0f, 1.0f);
}
else
{
cube.m_triangles[i].aV.color = glm::vec3(0.0f, 1.0f, 0.0f);
cube.m_triangles[i].bV.color = glm::vec3(0.0f, 1.0f, 0.0f);
cube.m_triangles[i].cV.color = glm::vec3(0.0f, 1.0f, 0.0f);
}
}
glm::mat4 mvpCube = proj * view * modelCube;
shaderBasic.SetUniformMat4f("u_MVP", mvpCube);
cube.DrawTriangle(shaderBasic);
modelPoint = glm::translate(glm::mat4(1.0f), pointPos);
glm::mat4 mvpPoint = proj * view * modelPoint;
shaderBasic.SetUniformMat4f("u_MVP", mvpPoint);
point.DrawTriangle(shaderBasic);
//gl_window.Unbind();
glfwSwapBuffers(gl_window.window);
glfwPollEvents();
}
The point is represented by a small yellow cube in the scene so that the dot can be seen more easily. At the same time, the position of the cube on the scene can be changed with the W, A, S, D, Q, E keys. When triangle and point intersection happened, the triangle that intersect with point will colored with white. That way we can see intersection on OpenGL scene easily.
Lastly here is our main algorithm. It retuns a bool. If point is inside of triangle it will return true if not it will return false.
bool CheckPointInTriangle(const Point& point, const Triangle& triangle)
{
glm::vec3 a = triangle.a - point;
glm::vec3 b = triangle.b - point;
glm::vec3 c = triangle.c - point;
glm::vec3 normPBC = glm::cross(b, c);
glm::vec3 normPCA = glm::cross(c, a);
glm::vec3 normPAB = glm::cross(a, b);
if (glm::dot(normPBC, normPCA) < 0.0f) {
return false;
}
else if (glm::dot(normPBC, normPAB) < 0.0f) {
return false;
}
return true;
}
For detailed explanation and little more theory check Gabor Szauer’s Game Physics Cookbook and his github repo.
I hope it helps. If you have any issues or question dont hesitate to contact with me.